Addition von Bewegungen

Nun ist es möglich mit mehreren Teilbewegungen eine neue Bewegung zu bilden. Dafür sind die Beträge der Geschwindigkeiten und ihre Richtungen erforderlich. Aus diesen Werten kann man den Betrag und die neue Richtung der Bewegung erkennen.

Es gibt 3 Möglichkeiten, wie die Bewegungen sich zueinander verhalten können.

  1. Sie laufen in die gleiche oder entgegengesetzte Richtung.
  2. Die Bewegungen laufen rechtwinklig zueinander ab.
  3. Die Bewegungen laufen in einem anderen Winkel zueinander ab. (siehe nächste Seite
i

Hinweis

Wir betrachten hier zwei gleichförmige Bewegungen.

Gleiche oder entgegengesetzte Richtung

Wenn die Bewegungen in die gleiche oder entgegengesetzte Richtung, kann man die Geschwindigkeiten einfach addieren.

!

Merke

Die Richtung der Bewegung bleibt gleich, ihr Betrag entsteht aus der Addition der Geschwindigkeiten.

Beispiel

Auf einem Förderband, das mit 4m/s fährt, bewegt sich in gleicher Richtung ein Modellauto mit 2m/s.

$v=4\frac{m}{s}+2\frac{m}{s}=6\frac{m}{s}$

i

Tipp

Bei entgegengesetzter Richtung ist eine Geschwindigkeit negativ:

Beispiel: Das Modellauto fährt in die entgegengesetzte Richtung: $v=4\frac{m}{s}+(-2\frac{m}{s})=2\frac{m}{s}$

Senkrecht zueinander

Wenn die Bewegungen senkrecht zueinander stehen, kann der Betrag mit Hilfe des Satzes des Pythagoras berechnet werden.

Beispiel

Das Modellauto fährt nun im rechten Winkel zum Rand über das Band.

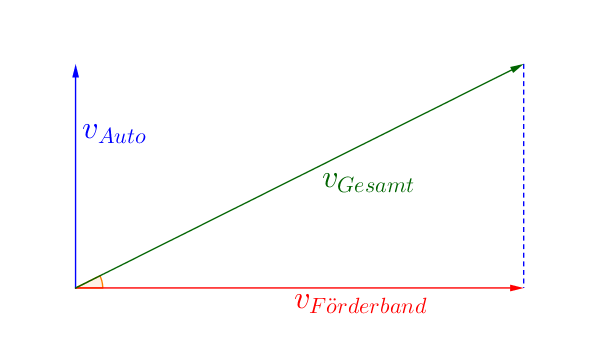
Um nun die Bewegung zu berechnen, nutzen wir:
Kathete²+Kathete²=Hypotenuse²

$v_\text{Gesamt}^2=v_\text{Auto}^2+v_\text{Band}^2$

$v_\text{Gesamt}^2=(2\frac{m}{s})^2+(4\frac{m}{s})^2$

$v_\text{Gesamt}=\sqrt{20\frac{m^2}{s^2}}$ $\approx4,47\frac{m}{s}$

Die neue Richtung lässt sich mit Hilfe des Arkustangens ($\tan^{-1}$ oder $\arctan$) bestimmen.

$\tan(\alpha)=\frac{v_\text{Auto}}{v_\text{Band}}$

$\alpha=\arctan(\frac{v_\text{Auto}}{v_\text{Band}})$

$\alpha=\arctan(\frac24)\approx26,6°$