Neben der Addtition von Bewegungen, die in die gleiche bzw. entgegengesetzte Richtung oder senkrecht verlaufen, lassen sich auch Bewegungen addieren, welche in einem anderen Winkel zueinander stehen.
Es gibt zwei Möglichkeiten zur Berechnung der resultierenden Geschwindigkeit:
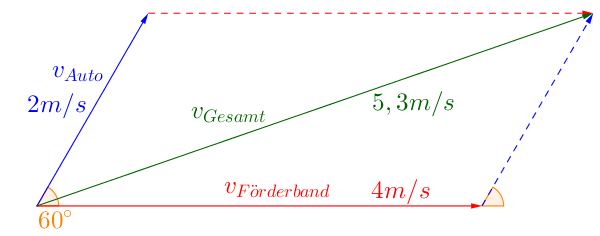
Auf einem Förderband, das mit 4m/s fährt, bewegt sich in einem Winkel von 60° zum Förderband ein Modellauto mit 2m/s.
Dabei muss $\alpha$ der Winkel zwischen den beiden Strecken $b$ und $c$ sein. Zusätzlich müssen diese mit $a$ ein Dreieck bilden.

Dadurch ist unser Winkel mit 60° an der falschen Stelle. Allerdings können wir den Winkel dazwischen mit 120° berechnen. Nun gilt:
$a^2=4^2+2^2-2\cdot2\cdot4\cdot\cos(120°)$
$a^2=20-16\cdot\cos(120°)$
$a^2=28$
$a\approx5,3\frac{m}s$